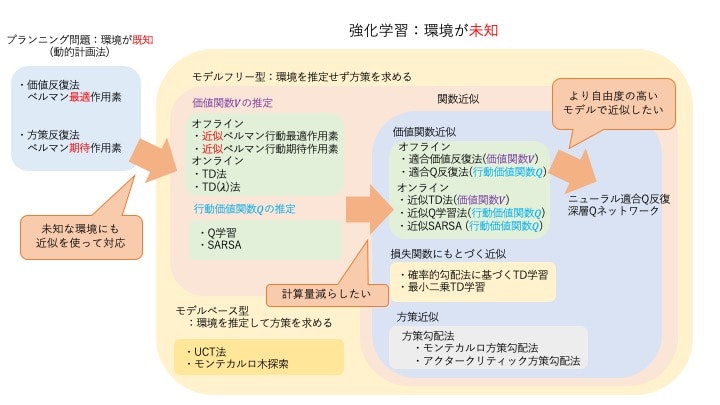
Planning Problems
Sequential decision-making problems where the environment dynamics (state transition probabilities and reward functions) are known.
Value Iteration Directly computes the optimal value function by repeatedly applying the Bellman optimality operator.
\[ (B_{\*}v)(s) = \max_a \{g(s,a) + \gamma \sum_{s'} p_T(s'|s,a)v(s')\} \]\[ V^{\*} = \lim_{k \to \infty} (B_{*}^{k}V)(s) \]Policy Iteration Iterates between two steps – “policy evaluation” and “policy improvement” – to find the optimal policy.
- Policy Evaluation: Computes the value function \(V^\pi\) under the current policy \(\pi\) using the Bellman expectation operator. \( (B_{\pi}v)(s) = \sum_a \pi(a|s) (g(s,a) + \gamma \sum_{s'} p_T(s'|s,a)v(s')) \) \( V^{\pi} = \lim_{k \to \infty} (B_{\pi}^{k}V)(s) \)
- Policy Improvement: Greedily determines a better policy using the computed value function \(V^\pi\). \( \pi(s) = \arg\max_a \{g(s,a) + \gamma \sum_{s'} p_T(s'|s,a)V^\pi(s')\} \)
Reinforcement Learning
Sequential decision-making problems where the environment dynamics are unknown. The agent collects data through interaction with the environment and learns the optimal policy from that data.
Value-Based Methods
These methods estimate a value function (state-value function V or action-value function Q) and implicitly derive a policy from it.
TD Learning (Temporal-Difference Learning) Fixes a policy \(\pi\) and estimates the state-value function V under it. The value function is updated online using the TD error \(\delta\).
\[ \delta_t = r_t + \gamma \hat{V}(s_{t+1}) - \hat{V}(s_t) \]\[ \hat{V}(s_t) \leftarrow \hat{V}(s_t) + \alpha_t \delta_t \]Q-Learning Estimates the action-value function Q. Since it uses the action
\[ \delta_t = r_t + \gamma \max_{a'} \hat{Q}(s_{t+1}, a') - \hat{Q}(s_t, a_t) \]\[ \hat{Q}(s_t, a_t) \leftarrow \hat{Q}(s_t, a_t) + \alpha_t \delta_t \]max_a'that maximizes the value of the next state for updates, it is an off-policy method that does not depend on the current policy.SARSA Estimates the action-value function Q. Unlike Q-Learning, the next action \(a_{t+1}\) is selected according to the current policy \(\pi\), making it an on-policy method.
\[ \delta_t = r_t + \gamma \hat{Q}(s_{t+1}, a_{t+1}) - \hat{Q}(s_t, a_t) \]\[ \hat{Q}(s_t, a_t) \leftarrow \hat{Q}(s_t, a_t) + \alpha_t \delta_t \]
Policy-Based Methods
These methods directly model and optimize the policy \(\pi_\theta\) with parameters \(\theta\), without going through a value function.
- Policy Gradient Methods Compute the gradient \(\nabla_\theta J(\theta)\) to maximize a performance measure \(J(\theta)\), and update the policy parameters \(\theta\). \( \theta_{t+1} = \theta_t + \alpha \nabla_\theta J(\theta_t) \)
Actor-Critic Methods
These methods combine value-based and policy-based approaches.
- Actor: Updates the policy \(\pi_\theta\) (selects actions)
- Critic: Learns a value function and evaluates the actions chosen by the actor
Both the actor and critic are updated using the TD error \(\delta_t\).
- Critic Update (Value Function Learning) \( \delta_t = r_t + \gamma \hat{V}_w(s_{t+1}) - \hat{V}_w(s_t) \) \( w_{t+1} = w_t + \alpha_w \delta_t \nabla_w \hat{V}_w(s_t) \)
- Actor Update (Policy Learning) \( \theta_{t+1} = \theta_t + \alpha_\theta \delta_t \nabla_\theta \log \pi_\theta(a_t|s_t) \)
Function Approximation
When the state space is large or continuous, value functions and policies are approximated using parameterized functions (such as linear functions or neural networks) with parameters \(w\) or \(\theta\), instead of tabular representations.
Value Function Approximation Combines function approximation with update rules such as TD learning and Q-Learning. For example, in approximate Q-Learning, the weights \(w\) are updated as follows:
\[ \delta_t = r_t + \gamma \max_{a'} \hat{Q}_w(s_{t+1}, a') - \hat{Q}_w(s_t, a_t) \]\[ w_{t+1} = w_t + \alpha_t \delta_t \nabla_w \hat{Q}_w(s_t, a_t) \]Deep Q-Network (DQN) uses a neural network to approximate the action-value function and stabilizes learning with techniques such as experience replay and target networks.
Policy Function Approximation Directly approximates the policy using function approximation in policy gradient methods and actor-critic methods.
References
- Tetsuro Morimura, “MLP Machine Learning Professional Series: Reinforcement Learning”