Information theory is a mathematical framework for quantifying, compressing, and communicating information. In machine learning, its concepts are applied in various contexts, including model evaluation and regularization.
Information Content
The “information content” \(h(x)\) gained from observing an event \(x\) is defined by how “surprising” the event is – that is, how low its probability \(p(x)\) is.
Information content is naturally defined to satisfy the following properties:
- Additivity: The information gained from observing two independent events \(x, y\) equals the sum of the information from each. \(h(x, y) = h(x) + h(y)\)
- Independence: The joint probability of independent events is the product of their individual probabilities. \(p(x, y) = p(x)p(y)\)
From these two properties, it follows that information content should be defined using the logarithm of the probability. A negative sign is added so that information content is non-negative (since \(p(x) \le 1\)).
\[ h(x) = -\log_2 p(x) \]When using base 2 for the logarithm, the unit of information is the bit.
Entropy
Entropy represents the average information content generated by a random variable \(X\). It is computed as the expected value of \(h(x)\) with respect to the distribution \(p(x)\).
\[ H[X] = \mathbb{E}\_{p(x)}[h(x)] = -\sum_x p(x) \log_2 p(x) \]Entropy can be interpreted as the degree of “uncertainty” or “unpredictability” of a random variable.
- Low entropy: The distribution is concentrated on a few specific values (sharp peak). Outcomes are easy to predict, so uncertainty is low.
- High entropy: The distribution is spread across many values (close to uniform). Outcomes are hard to predict, so uncertainty is high.
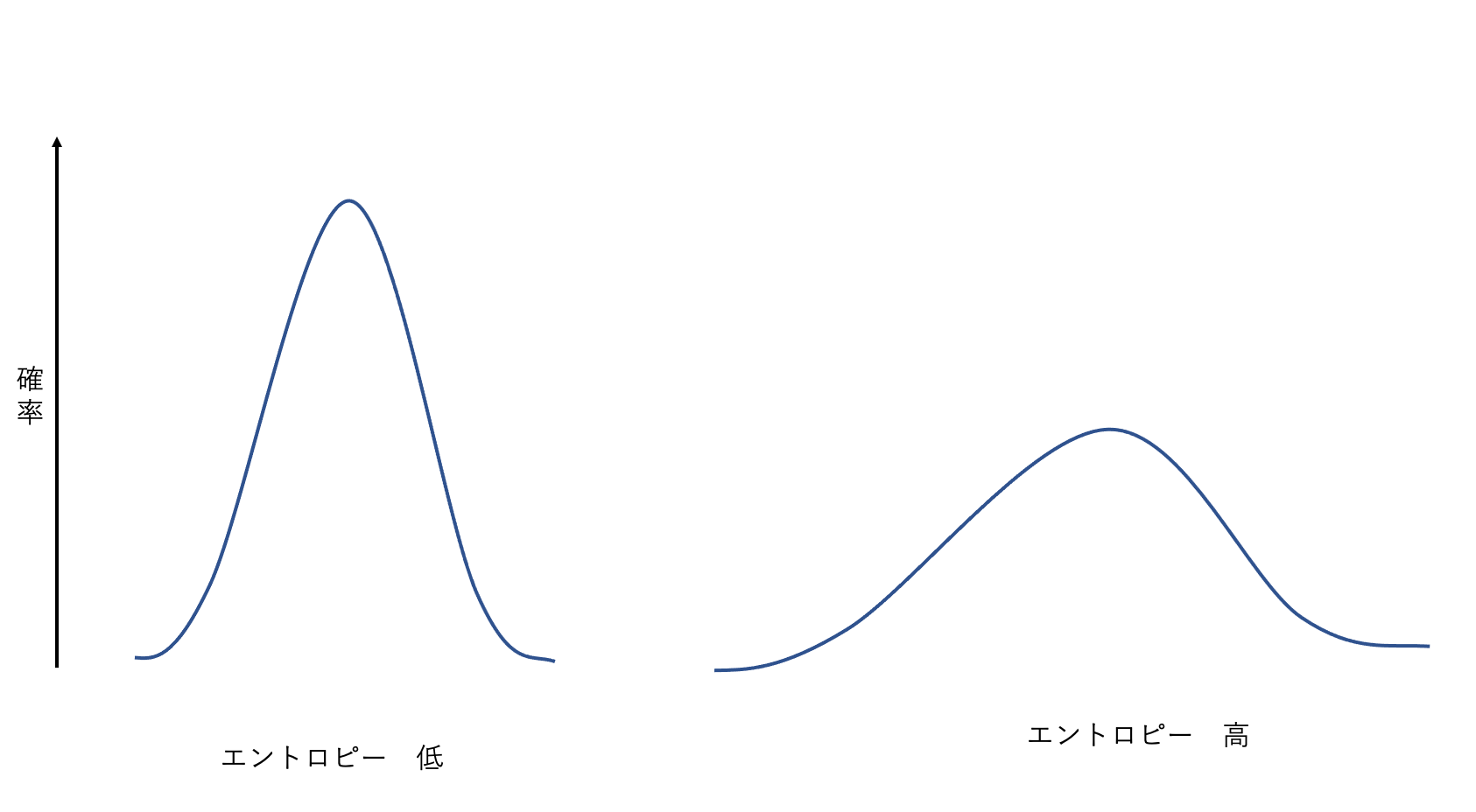
According to the noiseless coding theorem, entropy provides a lower bound on the number of bits needed to transmit the values of a random variable without error. For example, when encoding characters with unequal frequencies, assigning shorter codes to frequent characters and longer codes to rare ones brings the average code length close to the entropy.
Differential Entropy
The extension of entropy to continuous random variables is called differential entropy.
\[ H[X] = -\int p(x) \ln p(x) dx \]Note: Unlike its discrete counterpart, differential entropy can take negative values and does not represent an absolute quantity of information.
Maximizing Differential Entropy
Considering which distribution maximizes differential entropy under certain constraints reveals the nature of that random variable. For example, the distribution that maximizes differential entropy given fixed mean \(\mu\) and variance \(\sigma^2\) is the Gaussian distribution.
\[ p(x) = \frac{1}{\sqrt{2\pi\sigma^2}} \exp\lbrace-\frac{(x-\mu)^2}{2\sigma^2}\rbrace \]The differential entropy of a Gaussian distribution is:
\[ H[X] = \frac{1}{2} \{1 + \ln(2\pi\sigma^2)\} \]This shows that entropy increases with larger variance \(\sigma^2\) (greater spread of the distribution).
Conditional Entropy and Mutual Information
Conditional Entropy
Consider the joint distribution \(p(x, y)\) of two random variables \(X, Y\). Conditional entropy measures how much uncertainty remains about \(Y\) given that \(X = x\) is known.
\[ H[Y|X] = -\iint p(x, y) \ln p(y|x) dy dx \]These satisfy the chain rule of entropy:
\[ H[X, Y] = H[Y|X] + H[X] \]This can be interpreted as: “the information needed to determine both \(X\) and \(Y\) equals the information needed to determine \(X\) plus the additional information needed to determine \(Y\) given \(X\).”
Relative Entropy (Kullback-Leibler Divergence)
When approximating an unknown true distribution \(p(x)\) with a model \(q(x)\), the relative entropy or KL divergence is used to measure the “gap” between the two distributions.
\[ KL(p||q) = -\int p(x) \ln \lbrace \frac{q(x)}{p(x)} \rbrace dx \]KL divergence has the following important properties:
- \(KL(p||q) \ge 0\)
- \(KL(p||q) = 0\) if and only if \(p(x) = q(x)\)
This makes KL divergence interpretable as a “distance-like” measure between two distributions (though it is not a true mathematical distance since it lacks symmetry: \(KL(p||q) \neq KL(q||p)\)).
KL Divergence Minimization and Maximum Likelihood
When data is generated from an unknown distribution \(p(x)\) and we approximate it with a parameterized model \(q(x|\theta)\), the goal is to find \(\theta\) that minimizes the KL divergence between them.
Expanding \(KL(p||q)\):
\[ KL(p||q) = -\int p(x) \ln q(x|\theta) dx + \int p(x) \ln p(x) dx \]The second term is the entropy of the true distribution and does not depend on \(\theta\). Therefore, minimizing \(KL(p||q)\) is equivalent to maximizing the first term – the expected log-likelihood.
Given a dataset \(\{x_n\}\), this expectation can be approximated by the sample average, so minimizing KL divergence is equivalent to maximum likelihood estimation.
Mutual Information
Mutual information measures how strongly two random variables \(X, Y\) depend on each other – how much knowing one reduces the uncertainty about the other.
It is defined as the KL divergence between the joint distribution \(p(x, y)\) and the product of marginals \(p(x)p(y)\):
\[ I[X, Y] \equiv KL(p(x, y) || p(x)p(y)) = \iint p(x, y) \ln ( \frac{p(x, y)}{p(x)p(y)} ) dx dy \]Mutual information can also be expressed using entropy:
\[ I[X, Y] = H[X] - H[X|Y] = H[Y] - H[Y|X] \]This is interpreted as “the amount by which knowing \(Y\) reduces the uncertainty of \(X\).”
References
- C.M. Bishop, “Pattern Recognition and Machine Learning,” Springer (2006)