Particle Swarm Optimization (PSO) and Two-Swarm Cooperative PSO (TCPSO) with Matlab

Particle Swarm Optimization (PSO)

PSO is an optimization algorithm inspired by the flocking behavior of birds and fish. The swarm shares information about promising locations, and each individual adjusts its behavior based on both its own experience and the group’s experience, enabling efficient search for optimal solutions.

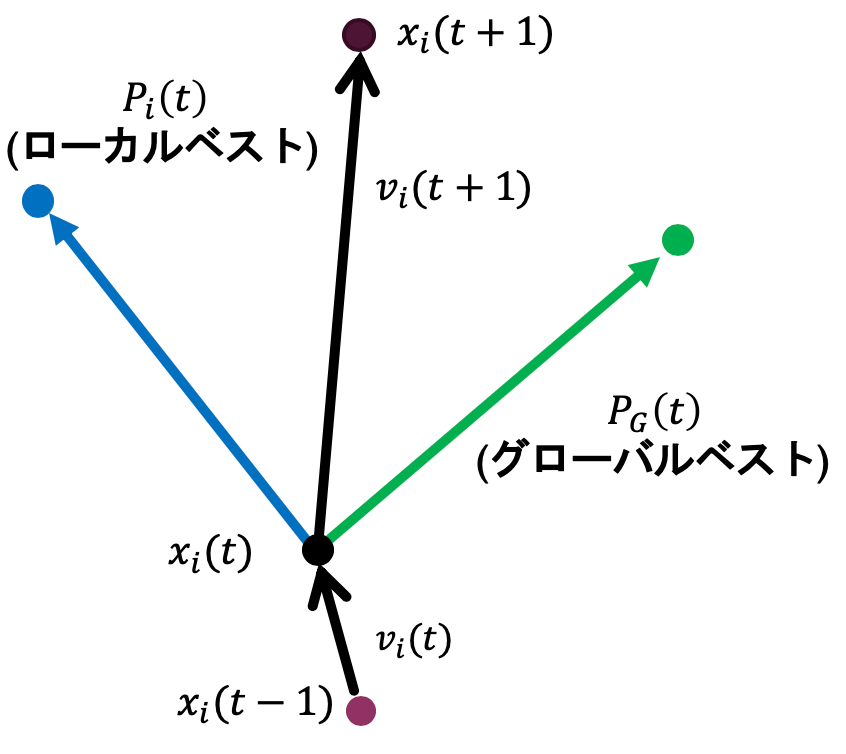
In PSO, search agents called “particles” fly through the search space carrying position and velocity information. Each particle determines its next velocity and position based on its own personal best position (pbest) and the global best position of the entire swarm (gbest).

Particle Update Rules

Let $x_i(t)$ and $v_i(t)$ denote the position and velocity of particle $i$ at time $t$. Let $P_i(t)$ be particle $i$’s personal best position and $P_G(t)$ be the global best position of the swarm. The velocity and position are updated as follows:

$$ v_i(t+1) = w \cdot v_i(t) + C_1 r_1 (P_i(t) - x_i(t)) + C_2 r_2 (P_G(t) - x_i(t)) $$

$$ x_i(t+1) = x_i(t) + v_i(t+1) $$

$w$: Inertia weight. Determines how much of the current velocity is retained.
$C_1$: Cognitive coefficient. The degree to which a particle moves toward its own personal best.
$C_2$: Social coefficient. The degree to which a particle moves toward the global best.
$r_1, r_2$: Uniform random numbers in [0, 1]. Introduce diversity in the search.

The update concept is illustrated in the following figure.

Challenges of PSO

While PSO is easy to implement, it is highly dependent on parameters. In particular, particles tend to cluster around the global best $P_G(t)$, making it prone to getting trapped in local optima. Balancing convergence speed and diversity maintenance is crucial.

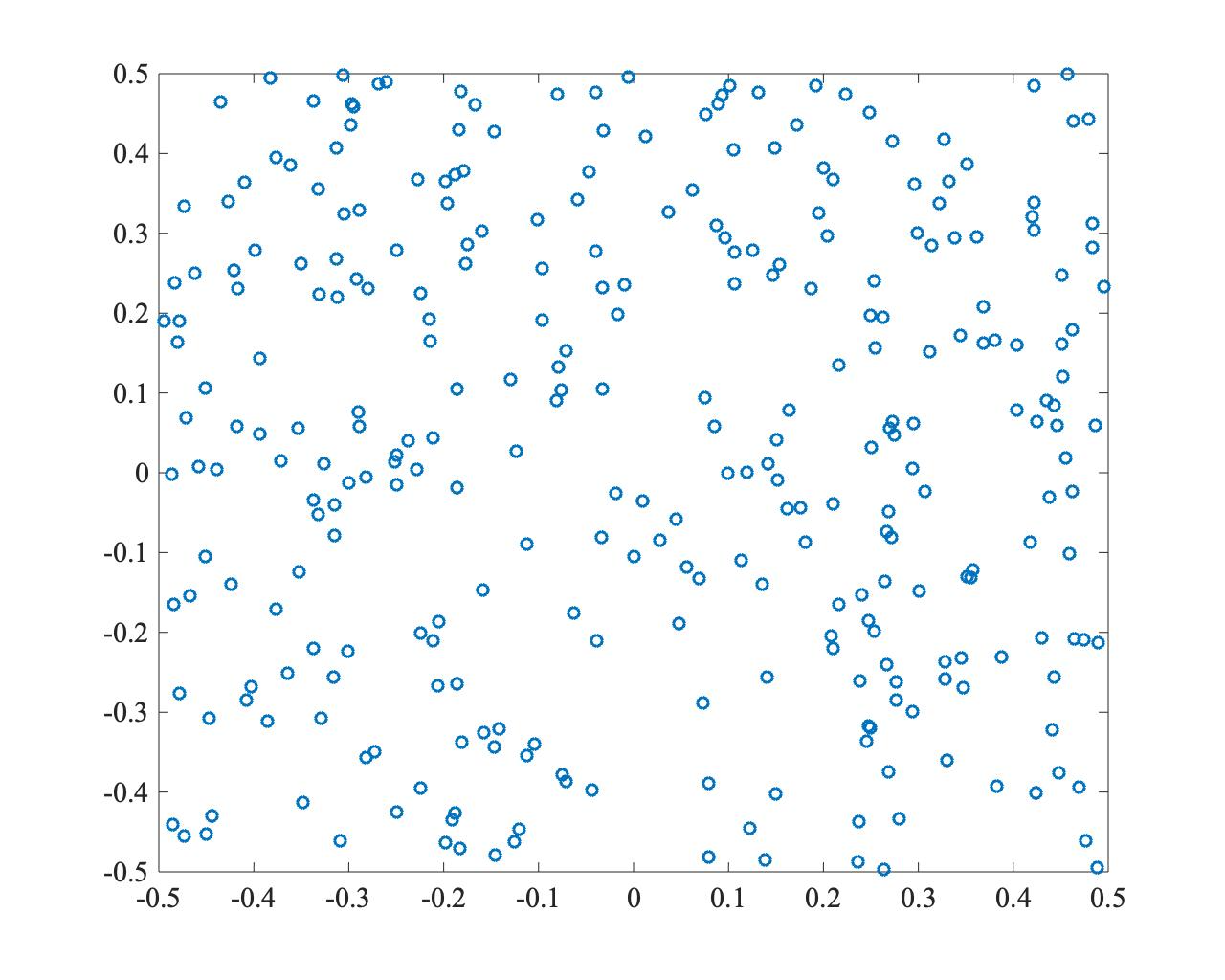
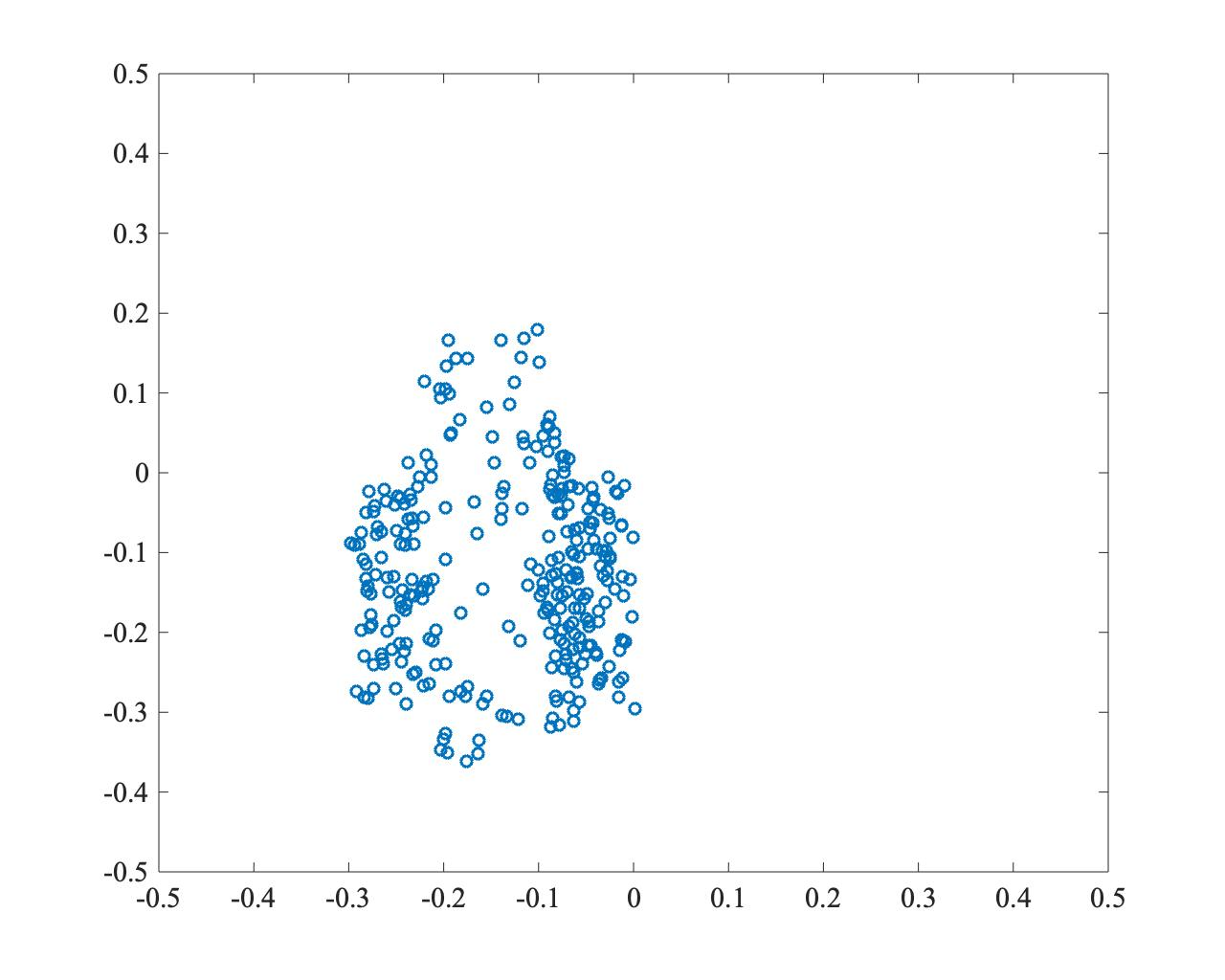
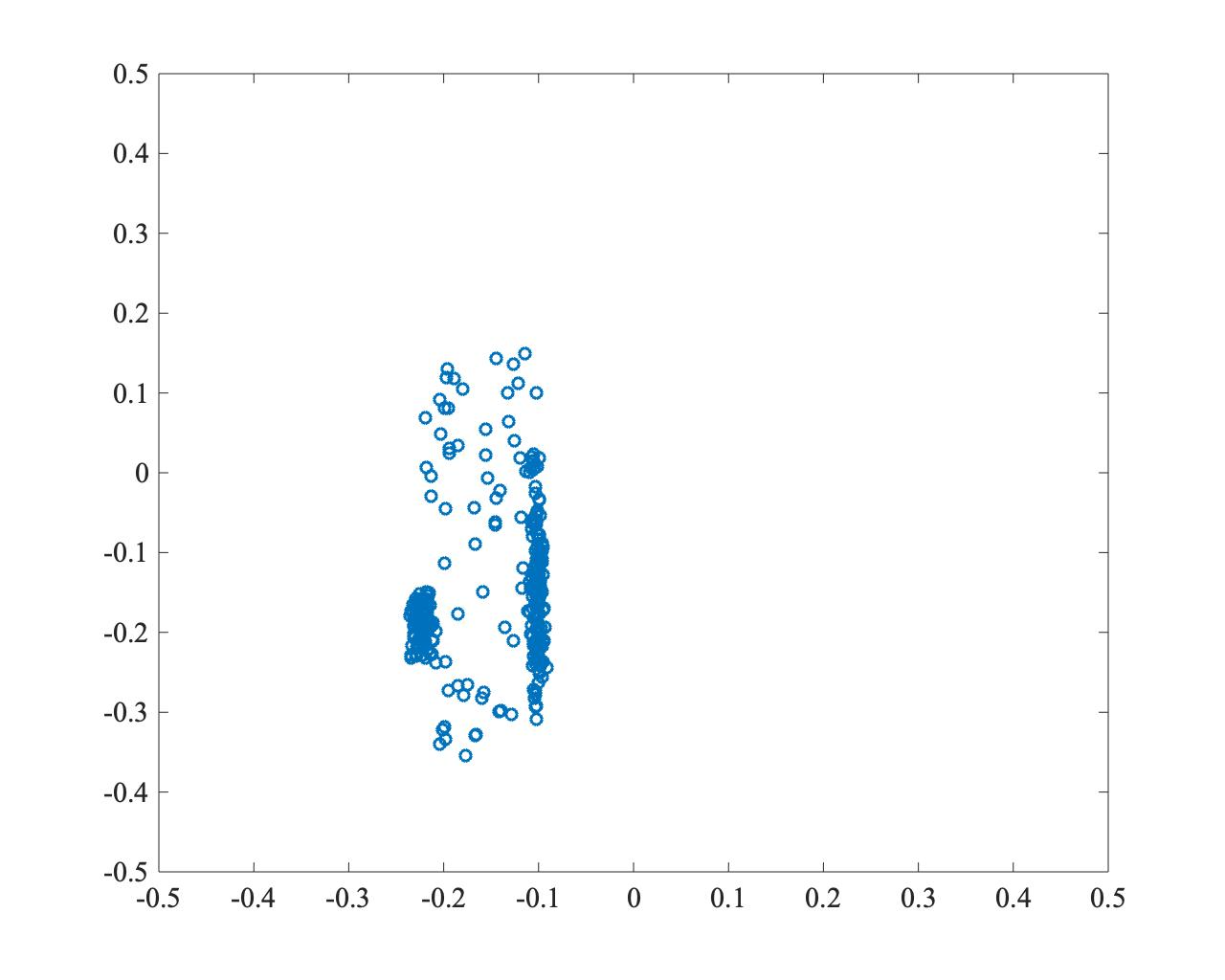
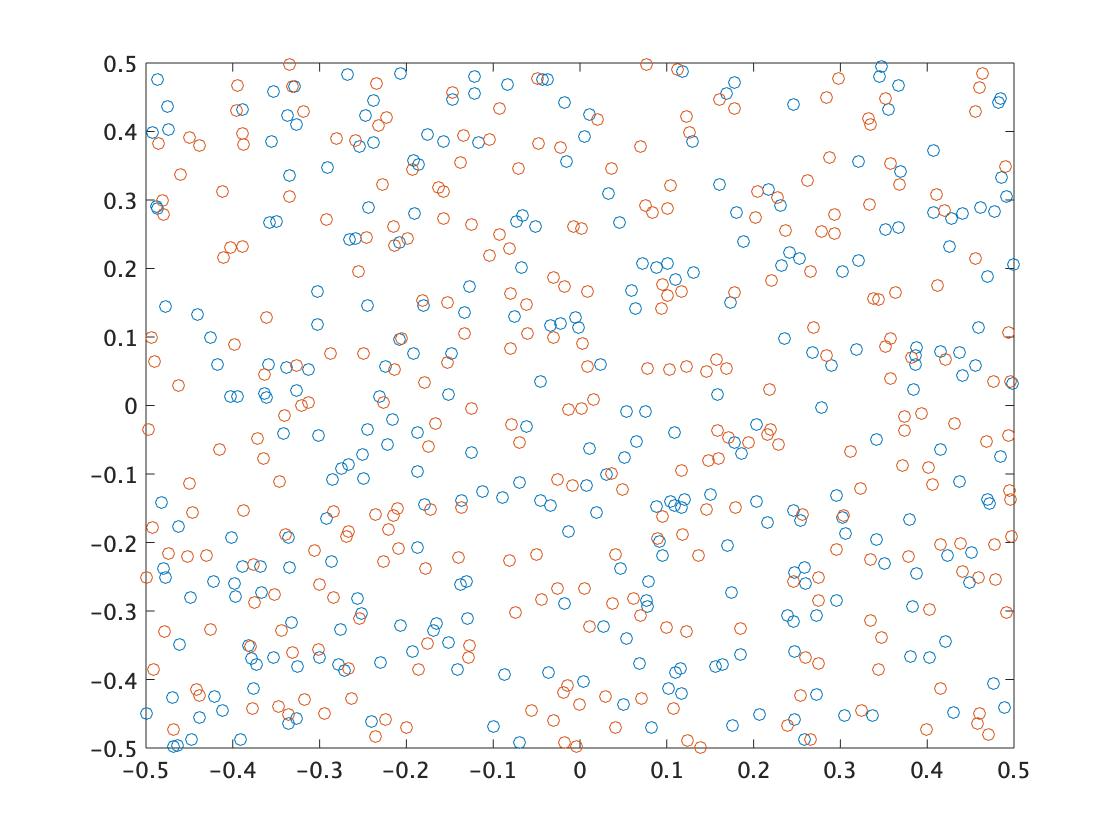
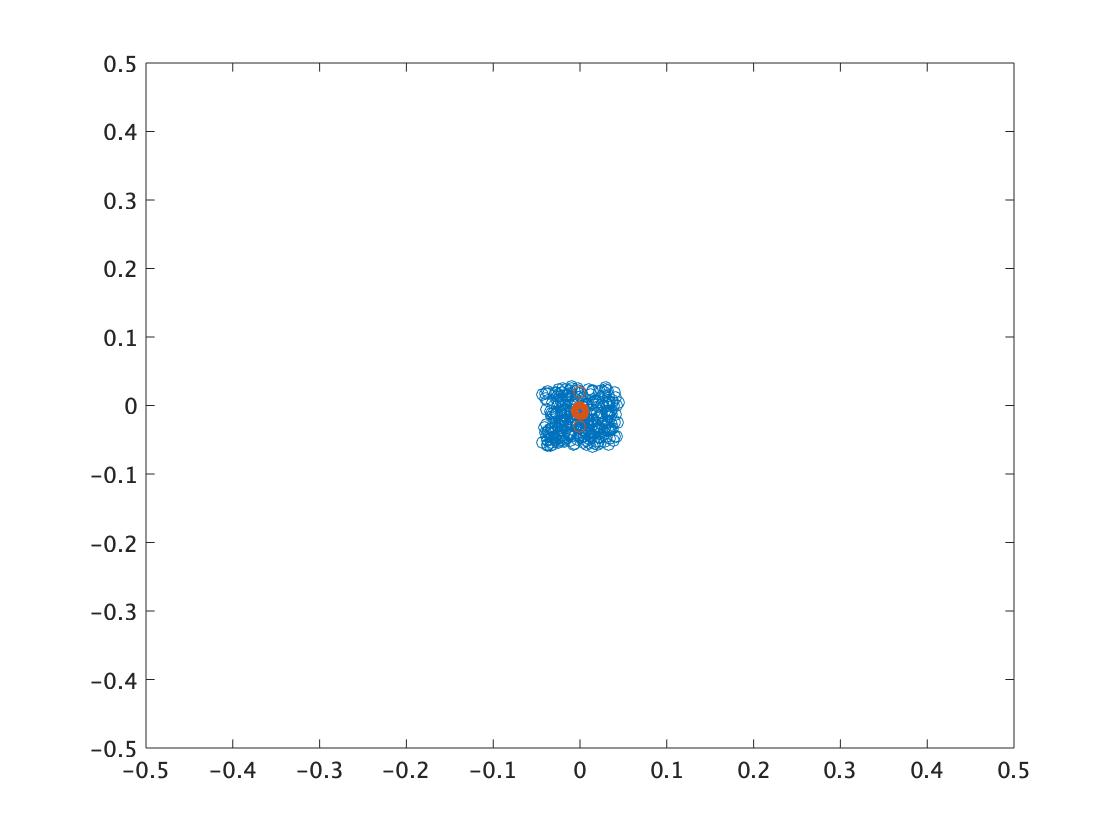
The following example shows PSO searching for the optimal solution at (0,0). While convergence is fast, the particles concentrate at one point, illustrating the local optima problem.

$t=0$
$t=250$
$t=500$

Two-Swarm Cooperative PSO (TCPSO)

TCPSO was proposed to address PSO’s convergence and diversity issues. Its key feature is the use of two particle swarms with different roles: a master swarm for global exploration and a slave swarm for intensive local search.

Particle Update Rules

Slave Swarm The slave swarm has no inertia term $w$ and is strongly attracted to the global best $P_G(t)$. This gives it the role of intensively exploring promising regions. $$ v_i^S(t+1) = C_1^S r_1 (P_i^S(t) - x_i^S(t)) + C_2^S r_2 (P_G(t) - x_i^S(t)) $$ $$ x_i^S(t+1) = x_i^S(t) + v_i^S(t+1) $$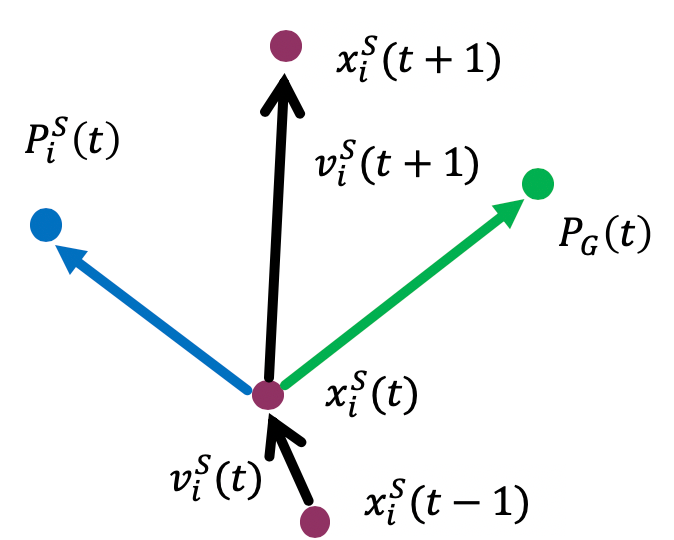
Master Swarm The master swarm also uses the slave swarm’s best position $P_G^S(t)$. This allows it to reference promising regions found by the slave swarm while maintaining search diversity through its inertia term. $$ v_i^M(t+1) = w^M v_i^M(t) + C_1^M r_1 (P_i^M(t) - x_i^M(t)) + C_2^M r_2 (P_G^S(t) - x_i^M(t)) + C_3^M r_3 (P_G(t) - x_i^M(t)) $$ $$ x_i^M(t+1) = x_i^M(t) + v_i^M(t+1) $$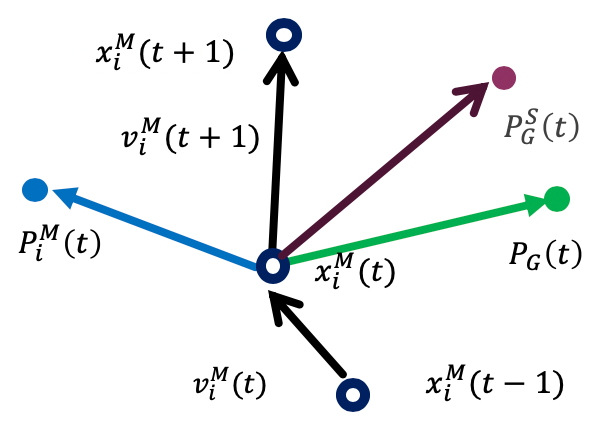

Properties of TCPSO

By combining the slave swarm’s fast convergence with the master swarm’s diversity maintenance, TCPSO achieves efficient search. However, in large-scale, high-dimensional problems, the master swarm may still converge to local optima.

The following shows a TCPSO execution example. Orange represents the slave swarm and blue represents the master swarm. The slave swarm quickly converges to a promising region while the master swarm maintains diversity around it.

$t=0$
$t=250$
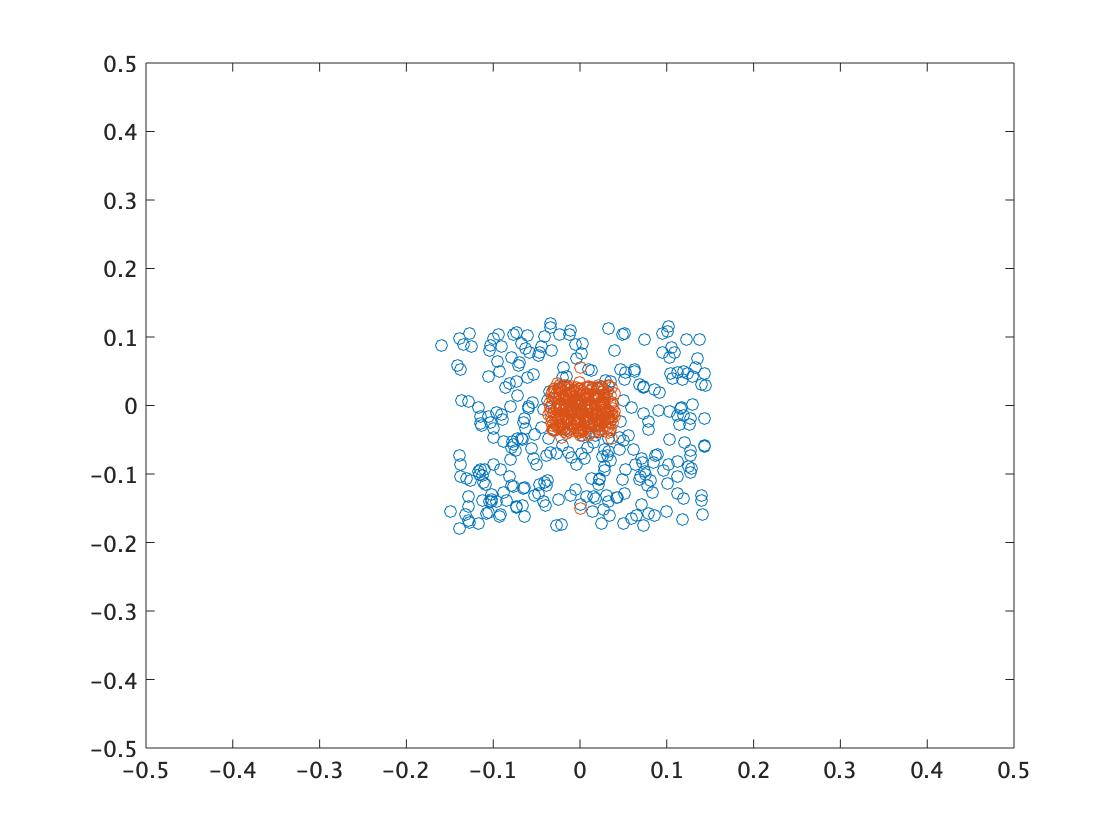
$t=500$

Matlab Programs

PSO

% PSO Parameters
ns = 300;       % Number of particles
c1 = 1.0;       % Cognitive coefficient
c2 = 1.0;       % Social coefficient
w = 0.9;        % Inertia weight
maxT = 500;     % Maximum iterations
D = 2;          % Problem dimension

% STEP1: Initialize particle swarm
ps = rand(ns, D) - 0.5; % Position initialized in [-0.5, 0.5]
ps_v = zeros(ns, D);   % Velocity initialized to 0
ps_fitness = zeros(ns, 1); % Fitness values

ps_best_pos = ps;      % Personal best positions (pbest)
ps_best_fitness = zeros(ns, 1); % Personal best fitness

g_best_pos = zeros(1, D); % Global best position (gbest)
g_best_fitness = -inf;    % Global best fitness

figure;

for t = 1:maxT
    % STEP2: Evaluate fitness
    % Fitness function: 1 / (abs(x) + abs(y)) (closer to origin = higher fitness)
    ps_fitness = 1 ./ (sum(abs(ps), 2) + 1e-9); % Avoid division by zero

    % STEP3: Update personal best (pbest)
    update_indices = ps_fitness > ps_best_fitness;
    ps_best_pos(update_indices, :) = ps(update_indices, :);
    ps_best_fitness(update_indices) = ps_fitness(update_indices);

    % STEP4: Update global best (gbest)
    [current_max_fitness, max_idx] = max(ps_fitness);
    if current_max_fitness > g_best_fitness
        g_best_fitness = current_max_fitness;
        g_best_pos = ps(max_idx, :);
    end

    % STEP5: Update velocity and position
    r1 = rand(ns, D);
    r2 = rand(ns, D);
    ps_v = w * ps_v + c1 * r1 .* (ps_best_pos - ps) + c2 * r2 .* (g_best_pos - ps);
    ps = ps + ps_v;

    % Plot progress
    if mod(t, 50) == 0 || t == 1
        plot(ps(:,1), ps(:,2), 'b.');
        hold on;
        plot(g_best_pos(1), g_best_pos(2), 'r*', 'MarkerSize', 10);
        hold off;
        xlim([-0.5 0.5]);
        ylim([-0.5 0.5]);
        title(['PSO at Iteration: ', num2str(t)]);
        drawnow;
    end
end

TCPSO

% TCPSO Parameters
ns = 150; % Number of slave particles
nm = 150; % Number of master particles
w = 0.9;  % Master swarm inertia weight
c1s = 1.0; c2s = 1.0; % Slave swarm coefficients
c1m = 1.0; c2m = 1.0; c3m = 1.0; % Master swarm coefficients
maxT = 500;
D = 2;

% STEP1: Initialize particle swarms
% Slave swarm
sp = rand(ns, D) - 0.5;
sp_v = zeros(ns, D);
sp_fitness = zeros(ns, 1);
sp_best_pos = sp;
sp_best_fitness = zeros(ns, 1);
s_gbest_pos = zeros(1, D); % Slave swarm gbest
s_gbest_fitness = -inf;

% Master swarm
mp = rand(nm, D) - 0.5;
mp_v = zeros(nm, D);
mp_fitness = zeros(nm, 1);
mp_best_pos = mp;
mp_best_fitness = zeros(nm, 1);

% Global
g_best_pos = zeros(1, D); % Overall gbest
g_best_fitness = -inf;

figure;

for t = 1:maxT
    % STEP2: Evaluate fitness
    sp_fitness = 1 ./ (sum(abs(sp), 2) + 1e-9);
    mp_fitness = 1 ./ (sum(abs(mp), 2) + 1e-9);

    % STEP3: Update personal best (pbest)
    update_s = sp_fitness > sp_best_fitness;
    sp_best_pos(update_s, :) = sp(update_s, :);
    sp_best_fitness(update_s) = sp_fitness(update_s);

    update_m = mp_fitness > mp_best_fitness;
    mp_best_pos(update_m, :) = mp(update_m, :);
    mp_best_fitness(update_m) = mp_fitness(update_m);

    % STEP4: Update global best
    % Slave swarm gbest
    [s_current_max, s_max_idx] = max(sp_fitness);
    if s_current_max > s_gbest_fitness
        s_gbest_fitness = s_current_max;
        s_gbest_pos = sp(s_max_idx, :);
    end

    % Overall gbest
    [m_current_max, m_max_idx] = max(mp_fitness);
    if m_current_max > g_best_fitness
        g_best_fitness = m_current_max;
        g_best_pos = mp(m_max_idx, :);
    end
    if s_gbest_fitness > g_best_fitness
        g_best_fitness = s_gbest_fitness;
        g_best_pos = s_gbest_pos;
    end

    % STEP5: Update velocity and position
    % Slave swarm
    r1s = rand(ns, D); r2s = rand(ns, D);
    sp_v = c1s * r1s .* (sp_best_pos - sp) + c2s * r2s .* (g_best_pos - sp);
    sp = sp + sp_v;

    % Master swarm
    r1m = rand(nm, D); r2m = rand(nm, D); r3m = rand(nm, D);
    mp_v = w * mp_v + c1m * r1m .* (mp_best_pos - mp) + c2m * r2m .* (s_gbest_pos - mp) + c3m * r3m .* (g_best_pos - mp);
    mp = mp + mp_v;

    % Plot progress
    if mod(t, 50) == 0 || t == 1
        plot(sp(:,1), sp(:,2), 'b.'); % Slave
        hold on;
        plot(mp(:,1), mp(:,2), 'g.'); % Master
        plot(g_best_pos(1), g_best_pos(2), 'r*', 'MarkerSize', 10);
        hold off;
        xlim([-0.5 0.5]);
        ylim([-0.5 0.5]);
        title(['TCPSO at Iteration: ', num2str(t)]);
        legend('Slave', 'Master', 'Gbest');
        drawnow;
    end
end