Introduction
This article explains how to use a Genetic Algorithm (GA) to train the weights and biases of a neural network (NN) that approximates a specific function. GA is an optimization method inspired by biological evolution, and it can be effective for complex problems where gradient-based methods are difficult to apply.
The target function to learn is:
\[ f(x,y) = \frac{\sin(x^2) / \cos(y) + x^2 - 5y + 30}{80} \]Genetic Algorithm (GA)
GA is a search algorithm that mimics the mechanisms of biological evolution, particularly the principle of “survival of the fittest.” It represents candidate solutions as a population of “individuals (genes)” and evolves them toward better solutions through repeated genetic operations.
Basic GA Algorithm
- Initialize Population: Randomly generate a population of individuals (in this case, NN weights and biases).
- Evaluate Fitness: Calculate the “fitness” of each individual, measuring how well it solves the problem. Here, lower error between NN output and training data means higher fitness.
- Selection (Reproduction): Select individuals so that those with higher fitness have more opportunities to pass their genes to the next generation.
- Crossover: Create new individuals (offspring) by exchanging parts of the genes between selected pairs. This combines promising elements from different solutions.
- Mutation: With a certain probability, randomly alter parts of an individual’s genes. This promotes escape from local optima and maintains diversity.
- Generational Replacement: Replace the current population with the newly generated individuals.
- Termination Check: Stop if the maximum number of generations is reached or a satisfactory solution is found. Otherwise, return to step 2.
Properties of GA
- Advantage: Since gradient information is not required, GA can be applied to a wide range of problems regardless of differentiability or continuity. It has global search capability and is less likely to get trapped in local optima.
- Challenge: The best individual’s information can be lost through genetic operations (especially crossover). Additionally, many parameters (population size, crossover rate, mutation rate, etc.) need tuning, and convergence is not guaranteed.
Python Implementation
A set of NN weights and biases is treated as one “gene,” and GA is used to optimize it.
Key Parameters
import numpy as np
import math
import random
import matplotlib.pyplot as plt
# Parameter settings
GENERATIONS = 100 # Number of generations
POPULATION_SIZE = 1000 # Population size (number of NNs)
NUM_TEACHER_DATA = 1000 # Number of training data points
# NN structure
NUM_INPUT = 2
NUM_HIDDEN = 2
NUM_OUTPUT = 1
# GA parameters
CROSSOVER_RATE = 0.8 # Crossover rate
MUTATION_RATE = 0.05 # Mutation rate
# Target function
def target_function(x, y):
# Add small value to avoid divergence when cos(y) is near 0
cos_y = math.cos(y)
if abs(cos_y) < 1e-6:
cos_y = 1e-6
return (math.sin(x*x) / cos_y + x*x - 5*y + 30) / 80
# Activation function
def sigmoid(x):
return 1.0 / (1.0 + np.exp(-x))
Neural Network Class
Defines the NN corresponding to each individual.
class NeuralNetwork:
def __init__(self):
# Randomly initialize weights and biases
self.w_ih = np.random.uniform(-1, 1, (NUM_INPUT, NUM_HIDDEN))
self.b_h = np.random.uniform(-1, 1, NUM_HIDDEN)
self.w_ho = np.random.uniform(-1, 1, (NUM_HIDDEN, NUM_OUTPUT))
self.b_o = np.random.uniform(-1, 1, NUM_OUTPUT)
self.fitness = 0.0 # Fitness
def predict(self, x):
# Forward propagation
hidden_layer_input = np.dot(x, self.w_ih) + self.b_h
hidden_layer_output = sigmoid(hidden_layer_input)
output_layer_input = np.dot(hidden_layer_output, self.w_ho) + self.b_o
# Output layer uses identity activation
return output_layer_input[0]
def calculate_fitness(self, teacher_inputs, teacher_outputs):
# Calculate mean squared error over all training data
error = 0.0
for i in range(len(teacher_inputs)):
prediction = self.predict(teacher_inputs[i])
error += (prediction - teacher_outputs[i]) ** 2
mean_squared_error = error / len(teacher_inputs)
# Define fitness so lower error = higher fitness
self.fitness = 1.0 / (mean_squared_error + 1e-9) # Avoid division by zero
GA Class
Implements GA operations (selection, crossover, mutation).
class GeneticAlgorithm:
def __init__(self):
self.population = [NeuralNetwork() for _ in range(POPULATION_SIZE)]
def run_generation(self, teacher_inputs, teacher_outputs):
# 1. Calculate fitness for all individuals
for individual in self.population:
individual.calculate_fitness(teacher_inputs, teacher_outputs)
# 2. Generate new generation
new_population = []
# Elitism: Keep the best individual unchanged
elite = max(self.population, key=lambda ind: ind.fitness)
new_population.append(elite)
while len(new_population) < POPULATION_SIZE:
# 3. Selection (roulette wheel selection)
parent1 = self._roulette_selection()
parent2 = self._roulette_selection()
# 4. Crossover
child1, child2 = self._crossover(parent1, parent2)
# 5. Mutation
self._mutate(child1)
self._mutate(child2)
new_population.extend([child1, child2])
self.population = new_population[:POPULATION_SIZE]
def _roulette_selection(self):
total_fitness = sum(ind.fitness for ind in self.population)
pick = random.uniform(0, total_fitness)
current = 0
for individual in self.population:
current += individual.fitness
if current > pick:
return individual
return self.population[-1]
def _crossover(self, parent1, parent2):
child1 = NeuralNetwork()
child2 = NeuralNetwork()
if random.random() < CROSSOVER_RATE:
# Randomly swap parameter sets (uniform crossover, simplified)
child1.w_ih, child2.w_ih = (parent1.w_ih, parent2.w_ih) if random.random() < 0.5 else (parent2.w_ih, parent1.w_ih)
child1.b_h, child2.b_h = (parent1.b_h, parent2.b_h) if random.random() < 0.5 else (parent2.b_h, parent1.b_h)
child1.w_ho, child2.w_ho = (parent1.w_ho, parent2.w_ho) if random.random() < 0.5 else (parent2.w_ho, parent1.w_ho)
child1.b_o, child2.b_o = (parent1.b_o, parent2.b_o) if random.random() < 0.5 else (parent2.b_o, parent1.b_o)
else:
child1, child2 = parent1, parent2 # No crossover
return child1, child2
def _mutate(self, individual):
# Replace each weight/bias with probability MUTATION_RATE
for w in [individual.w_ih, individual.b_h, individual.w_ho, individual.b_o]:
if random.random() < MUTATION_RATE:
w += np.random.uniform(-0.1, 0.1, w.shape)
Main Function
def main():
# Generate training data
teacher_inputs = np.random.uniform(-5, 5, (NUM_TEACHER_DATA, NUM_INPUT))
teacher_outputs = np.array([target_function(x[0], x[1]) for x in teacher_inputs])
# Generate test data
test_inputs = np.random.uniform(-5, 5, (NUM_TEACHER_DATA, NUM_INPUT))
test_outputs = np.array([target_function(x[0], x[1]) for x in test_inputs])
ga = GeneticAlgorithm()
elite_errors = []
print("Training started...")
for gen in range(GENERATIONS):
ga.run_generation(teacher_inputs, teacher_outputs)
# Find the best individual (elite)
elite = max(ga.population, key=lambda ind: ind.fitness)
# Evaluate elite on test data
test_error = 0.0
for i in range(len(test_inputs)):
prediction = elite.predict(test_inputs[i])
test_error += (prediction - test_outputs[i]) ** 2
mean_squared_error = test_error / len(test_inputs)
elite_errors.append(mean_squared_error)
if (gen + 1) % 10 == 0:
print(f"Generation: {gen + 1}, Test Error (MSE): {mean_squared_error:.6f}")
# Plot results
plt.plot(elite_errors)
plt.title("Elite Individual's Error on Test Data")
plt.xlabel("Generation")
plt.ylabel("Mean Squared Error")
plt.grid(True)
plt.savefig("ga_nn_learning_curve.png")
plt.show()
if __name__ == '__main__':
main()
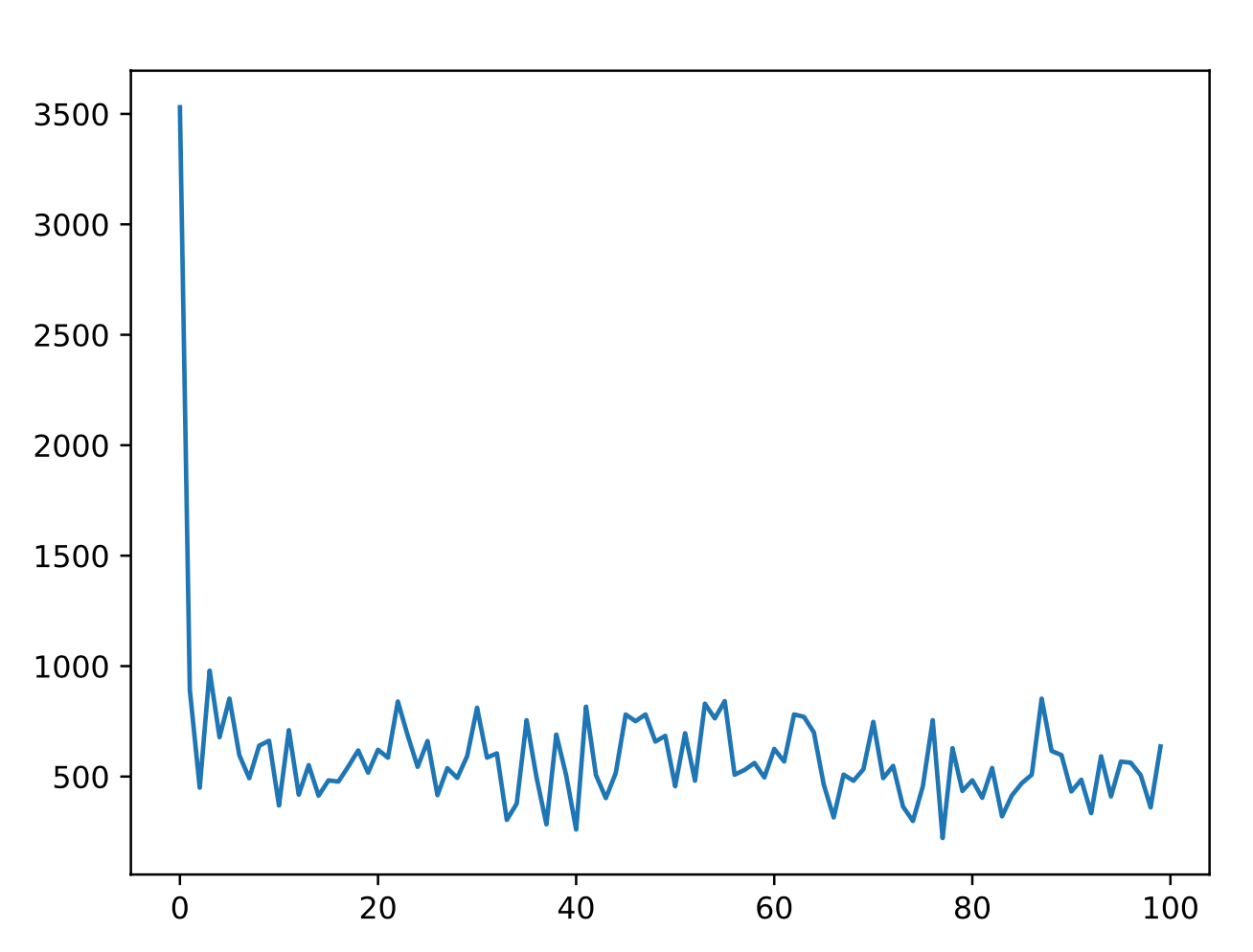
Experimental Results
The elite individual (highest fitness) from each generation was evaluated on test data, and the mean squared error was plotted. As generations progress, the error decreases, confirming that the NN is learning the function.