In Bayesian estimation, the combination of the likelihood function and the prior distribution is crucial for obtaining the posterior distribution analytically. A prior distribution that causes the posterior distribution to have the same functional form as itself for a given likelihood function is called a conjugate prior distribution. Using conjugate priors greatly simplifies the computation of the posterior distribution.
Representative Conjugate Prior Distributions
Dirichlet Distribution
The conjugate prior for the parameters (category probabilities) of the multinomial distribution is the Dirichlet distribution \(\mathcal{D}(\mu|\alpha)\).
\[ \mathcal{D}(\mu|\alpha) = \frac{\Gamma(\sum*{j=1}^{k}\alpha_j)}{\prod*{j=1}^k\Gamma(\alpha*j)}\prod*{j=1}^k\mu_j^{\alpha_j-1} \]Here, \(\alpha = (\alpha_1, \dots, \alpha_k)\) is the parameter of the Dirichlet distribution, and \(\Gamma(\cdot)\) is the Gamma function. The Gamma function extends the concept of factorial to real numbers and is defined as:
\[ \Gamma(x) = \int_0^\infty t^{x-1}e^{-t}dt \]Beta Distribution
The conjugate prior for the parameter (success probability) of the binomial distribution is the Beta distribution \(p(\mu|a,b)\).
\[ p(\mu|a,b) = \frac{1}{B(a,b)}\mu^{a-1}(1-\mu)^{b-1} \]Here, \(a, b\) are the parameters of the Beta distribution, and \(B(a,b)\) is the Beta function, defined as:
\[ B(a,b) = \int_0^1\mu^{a-1}(1-\mu)^{b-1}d\mu \]Gamma Distribution
The conjugate prior for the inverse of the variance (precision parameter) of the normal distribution is the Gamma distribution \(\mathcal{G}(\lambda|\kappa,\xi)\).
\[ \mathcal{G}(\lambda|\kappa,\xi) = \frac{\xi^\kappa}{\Gamma(\kappa)}\lambda^{\kappa-1}\exp(-\xi\lambda) \]Here, \(\lambda = 1/\sigma^2\) is the precision parameter, \(\kappa\) is the shape parameter, and \(\xi\) is the scale parameter (or the inverse of the rate parameter).
Note: The conjugate prior for the mean parameter of the normal distribution is itself a normal distribution. However, if a normal distribution is used as a prior for the variance parameter, the posterior distribution does not take the form of a normal distribution, so it is not conjugate. Therefore, the precision parameter (inverse of variance) is introduced, and the Gamma distribution is used as its conjugate prior.
Aside on the Gamma Distribution
- The Gamma distribution with \(\kappa=1\) is identical to the exponential distribution. \( \mathcal{G}(\lambda|1,\xi) = \frac{\xi^1}{\Gamma(1)}\lambda^{1-1}\exp(-\xi\lambda) = \xi\exp(-\xi\lambda) \) (\(\Gamma(1)=1\))
- Setting \(\xi=\frac{1}{2}\) and defining the parameter \(\nu=2\kappa\) gives the chi-squared distribution \(\chi^2(\lambda|\nu)\). \( \chi^2(\lambda|\nu) = \mathcal{G}(\lambda|\frac{\nu}{2},\frac{1}{2}) \)
Normal-Gamma Distribution
When estimating both the mean \(\mu\) and precision \(\lambda\) of the normal distribution simultaneously, the Normal-Gamma distribution \(\mathcal{NG}(\mu,\lambda|\psi,\beta,\kappa,\xi)\) can be used as their joint prior distribution. It has a structure where the mean \(\mu\) follows a normal distribution and the precision \(\lambda\) follows a Gamma distribution.
\[ \mathcal{NG}(\mu,\lambda|\psi,\beta,\kappa,\xi) = \mathcal{N}(\mu|\psi,(\beta \lambda)^{-1}) \mathcal{G}(\lambda|\kappa,\xi) \]Summary of Likelihood Functions and Their Conjugate Priors
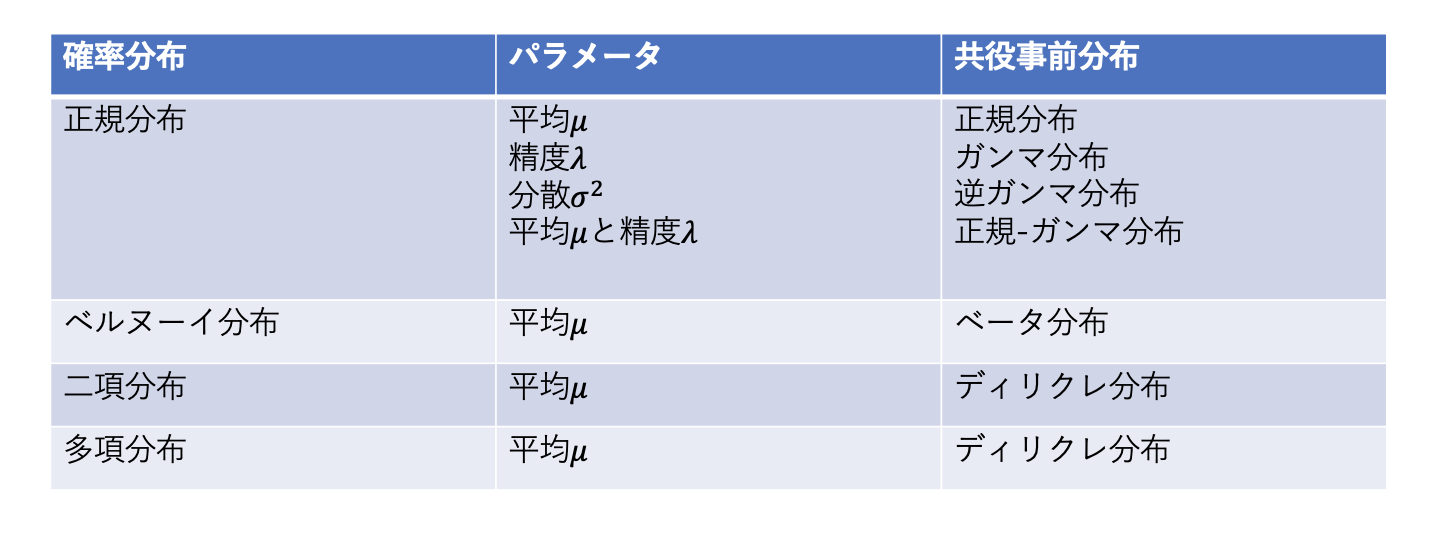
| Likelihood Function (Data Distribution) | Parameter | Conjugate Prior |
|---|---|---|
| Bernoulli distribution | Success probability \(\mu\) | Beta distribution |
| Binomial distribution | Success probability \(\mu\) | Beta distribution |
| Categorical distribution | Category probabilities \(\mu\) | Dirichlet distribution |
| Multinomial distribution | Category probabilities \(\mu\) | Dirichlet distribution |
| Normal distribution | Mean \(\mu\) | Normal distribution |
| Normal distribution | Precision \(\lambda\) | Gamma distribution |
| Normal distribution | Mean \(\mu\), Precision \(\lambda\) | Normal-Gamma distribution |
References
- Taro Tezuka, “Understanding Bayesian Statistics and Machine Learning,” Kodansha (2017)