Methods that apply deep neural networks (DNN) to reinforcement learning are broadly classified into three categories: “value-based,” “policy-based,” and “Actor-Critic,” which combines both.
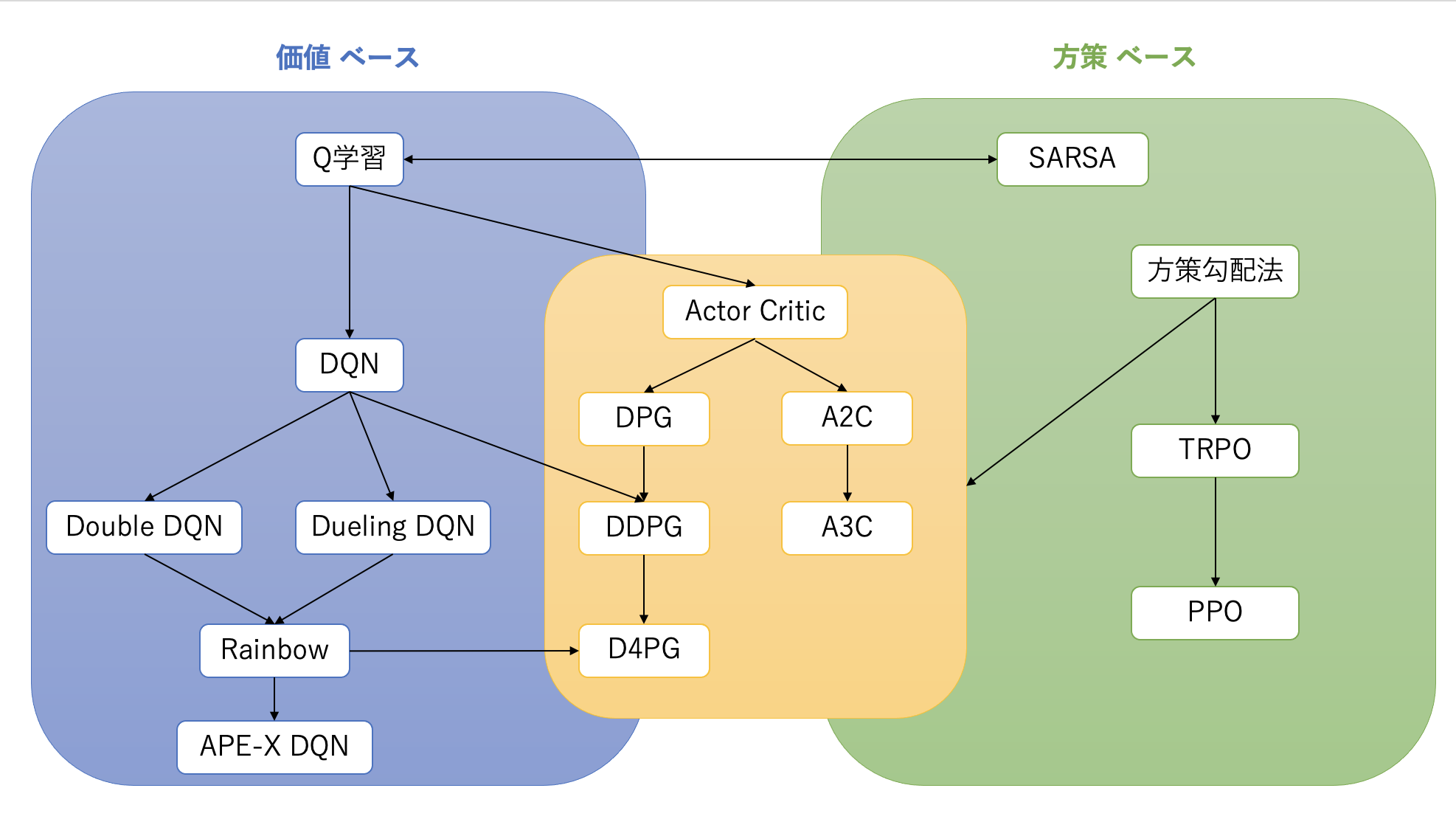
Actor-Critic Algorithms
The Actor-Critic method simultaneously learns a policy (Actor) and a value function (Critic).
Asynchronous Advantage Actor-Critic (A3C)
A3C is an asynchronous extension of A2C (Advantage Actor-Critic). Multiple agents collect experience and learn in parallel across different environments.
- Asynchronous Learning: Each agent copies parameters from the central global network, collects experience in its own environment while computing gradients, and then asynchronously applies the computed gradients to update the global network.
- Comparison with Experience Replay: While Experience Replay stores experience collected by a single agent in a buffer for learning, A3C ensures experience diversity by having multiple agents simultaneously collect experience in different environments. This reduces correlations between experiences and stabilizes learning.
- Origin of A2C: After A3C was published, it was shown that asynchrony does not necessarily contribute to performance improvement, and A2C was proposed, which synchronously collects gradients from multiple agents for updates. A2C is simpler to implement than A3C and often performs equally well or better.
Deep Deterministic Policy Gradient (DDPG)
DDPG is an Actor-Critic algorithm designed for continuous action spaces. While DQN was specialized for discrete action spaces, DDPG can output continuous actions.
- Deterministic Policy: Instead of outputting an action probability distribution, the Actor directly outputs a deterministic action from the state.
- Use of Experience Replay: Like DQN, Experience Replay is used to stabilize learning.
- Target Networks: Like DQN, target networks (for both Actor and Critic) are used for learning stabilization.
- TD Error: The Critic updates the value function using TD error, and this information is used for the Actor’s policy update.
Deterministic Policy Gradient (DPG)
DPG is the foundational algorithm for DDPG, which computes the gradient of a deterministic policy. DDPG combines DPG with deep learning and DQN’s stabilization techniques (Experience Replay, target networks).
Policy Gradient Algorithms
Policy gradient methods directly update policy parameters to maximize expected reward. However, they face the challenge of unstable learning.
Trust Region Policy Optimization (TRPO)
TRPO is a method to improve the stability of policy gradient learning. When updating the policy, it imposes a trust region constraint to prevent the updated policy from deviating too far from the previous policy.
- Constraint: The KL divergence between the updated policy \(\pi_\theta\) and the previous policy \(\pi_{\theta_{old}}\) is constrained to be below a threshold \(\delta\). \( \mathbb{E}_{s \sim d^{\pi_{\theta*{old}}}}[KL[\pi*{\theta*{old}}(\cdot|s),\pi*\theta(\cdot|s)]] ] \le \delta \)
- Objective Function: Under this constraint, it maximizes an objective function using the advantage function \(A_t\). \( \max*\theta \mathbb{E}*{s*t, a_t \sim \pi*{\theta*{old}}}\left[\frac{\pi*\theta(a*t|s_t)}{\pi*{\theta*{old}}(a_t|s_t)} A_t\right] \) Here, \(\frac{\pi*\theta(a*t|s_t)}{\pi*{\theta\_{old}}(a_t|s_t)}\) is called the probability ratio, representing the ratio of action selection probabilities before and after the update.
TRPO has theoretical guarantees but faces the challenge of complex implementation.
Proximal Policy Optimization (PPO)
PPO is an algorithm that maintains TRPO’s performance while simplifying the implementation. Instead of solving TRPO’s complex constrained optimization problem, it introduces clipping to the objective function.
- Clipping: The probability ratio \(\frac{\pi_\theta(a_t|s_t)}{\pi_{\theta_{old}}(a_t|s_t)}\) is restricted to a certain range (e.g., \([1-\epsilon, 1+\epsilon]\)). If it exceeds this range, the value is clipped. \( L^{CLIP}(\theta) = \mathbb{E}_{s_t, a_t \sim \pi_{\theta*{old}}}\left[\min\left(\frac{\pi*\theta(a*t|s_t)}{\pi*{\theta*{old}}(a_t|s_t)} A_t, \text{clip}\left(\frac{\pi*\theta(a*t|s_t)}{\pi*{\theta\_{old}}(a_t|s_t)}, 1-\epsilon, 1+\epsilon\right) A_t\right)\right] \) Maximizing this objective function stabilizes policy updates and has been shown to achieve performance equal to or better than TRPO. PPO is one of the most widely used reinforcement learning algorithms today due to its ease of implementation and high performance.
References
- Takahiro Kubo, “Introduction to Reinforcement Learning with Python: From Basics to Practice”, Shoeisha (2019)