はじめに
本記事では、遺伝的アルゴリズム(GA)を用いて、特定の関数を近似するニューラルネットワーク(NN)の重みとバイアスを学習させるプロセスを解説します。GAは、生物の進化を模倣した最適化手法であり、勾配法が適用しにくい複雑な問題に対しても有効な場合があります。
学習対象の関数は以下の通りです。
\[ f(x,y) = \frac{\sin(x^2) / \cos(y) + x^2 - 5y + 30}{80} \]遺伝的アルゴリズム (GA: Genetic Algorithm)
GAは、生物の進化のメカニズム、特に「適者生存」の原則を模倣した探索アルゴリズムです。解の候補を「個体(遺伝子)」の集団として表現し、以下の遺伝的操作を繰り返すことで、より良い解へと進化させていきます。
GAの基本アルゴリズム
- 初期集団の生成: 解の候補となる個体(本記事ではNNの重みとバイアス)の集団をランダムに生成します。
- 適応度の計算: 各個体がどの程度問題に適しているかを評価する「適応度」を計算します。今回は、NNの出力と教師データとの誤差が小さいほど適応度が高くなります。
- 選択(再生): 適応度が高い個体ほど、次世代に遺伝子を残す機会が多くなるように個体を選択します。
- 交叉: 選択された個体のペアから、遺伝子の一部を交換することで新しい個体(子)を生成します。これにより、有望な解の要素が組み合わさることが期待されます。
- 突然変異: 一定の確率で、個体の遺伝子の一部をランダムに変化させます。これにより、局所解からの脱出や多様性の維持を促します。
- 世代交代: 新しく生成された個体群で、既存の個体群を置き換えます。
- 終了条件の判定: 設定した世代数に達するか、満足のいく解が得られたら終了します。そうでなければ、ステップ2に戻ります。
GAの性質
- 利点: 勾配情報が不要なため、関数の微分可能性や連続性を問わず、広範な問題に適用できます。大域的な探索能力があり、局所解に陥りにくいとされています。
- 課題: 最良の個体の情報が遺伝的操作(特に交叉)によって失われることがあります。また、多くのパラメータ(集団サイズ、交叉率、突然変異率など)の調整が必要であり、収束が保証されない点も課題です。
Pythonによる実装
NNの重みとバイアスのセットを一つの「遺伝子」とみなし、GAを用いてこの遺伝子を最適化します。
主要なパラメータ
import numpy as np
import math
import random
import matplotlib.pyplot as plt
# パラメータ設定
GENERATIONS = 100 # 世代数
POPULATION_SIZE = 1000 # 集団の個体数(NNの数)
NUM_TEACHER_DATA = 1000 # 教師データの数
# NNの構造
NUM_INPUT = 2
NUM_HIDDEN = 2
NUM_OUTPUT = 1
# GAのパラメータ
CROSSOVER_RATE = 0.8 # 交叉率
MUTATION_RATE = 0.05 # 突然変異率
# 学習対象の関数
def target_function(x, y):
# cos(y)が0に近づくと発散するため、小さな値を加える
cos_y = math.cos(y)
if abs(cos_y) < 1e-6:
cos_y = 1e-6
return (math.sin(x*x) / cos_y + x*x - 5*y + 30) / 80
# 活性化関数
def sigmoid(x):
return 1.0 / (1.0 + np.exp(-x))
ニューラルネットワークのクラス
各個体に対応するNNをクラスとして定義します。
class NeuralNetwork:
def __init__(self):
# 重みとバイアスをランダムに初期化
self.w_ih = np.random.uniform(-1, 1, (NUM_INPUT, NUM_HIDDEN))
self.b_h = np.random.uniform(-1, 1, NUM_HIDDEN)
self.w_ho = np.random.uniform(-1, 1, (NUM_HIDDEN, NUM_OUTPUT))
self.b_o = np.random.uniform(-1, 1, NUM_OUTPUT)
self.fitness = 0.0 # 適応度
def predict(self, x):
# 順伝播計算
hidden_layer_input = np.dot(x, self.w_ih) + self.b_h
hidden_layer_output = sigmoid(hidden_layer_input)
output_layer_input = np.dot(hidden_layer_output, self.w_ho) + self.b_o
# 出力層の活性化関数は恒等関数とする
return output_layer_input[0]
def calculate_fitness(self, teacher_inputs, teacher_outputs):
# 全ての教師データに対する平均二乗誤差を計算
error = 0.0
for i in range(len(teacher_inputs)):
prediction = self.predict(teacher_inputs[i])
error += (prediction - teacher_outputs[i]) ** 2
mean_squared_error = error / len(teacher_inputs)
# 誤差が小さいほど適応度が高くなるように定義
self.fitness = 1.0 / (mean_squared_error + 1e-9) # 0除算を避ける
GAのクラス
GAの操作(選択、交叉、突然変異)を実装します。
class GeneticAlgorithm:
def __init__(self):
self.population = [NeuralNetwork() for _ in range(POPULATION_SIZE)]
def run_generation(self, teacher_inputs, teacher_outputs):
# 1. 全個体の適応度を計算
for individual in self.population:
individual.calculate_fitness(teacher_inputs, teacher_outputs)
# 2. 新しい世代を生成
new_population = []
# エリート選択: 最も優れた個体をそのまま次世代に残す
elite = max(self.population, key=lambda ind: ind.fitness)
new_population.append(elite)
while len(new_population) < POPULATION_SIZE:
# 3. 選択 (ルーレット選択)
parent1 = self._roulette_selection()
parent2 = self._roulette_selection()
# 4. 交叉
child1, child2 = self._crossover(parent1, parent2)
# 5. 突然変異
self._mutate(child1)
self._mutate(child2)
new_population.extend([child1, child2])
self.population = new_population[:POPULATION_SIZE]
def _roulette_selection(self):
total_fitness = sum(ind.fitness for ind in self.population)
pick = random.uniform(0, total_fitness)
current = 0
for individual in self.population:
current += individual.fitness
if current > pick:
return individual
return self.population[-1]
def _crossover(self, parent1, parent2):
child1 = NeuralNetwork()
child2 = NeuralNetwork()
if random.random() < CROSSOVER_RATE:
# 重みとバイアスの各要素をランダムに交換(一様交叉)
# (実装を簡略化するため、ここではパラメータセット全体を交換)
child1.w_ih, child2.w_ih = (parent1.w_ih, parent2.w_ih) if random.random() < 0.5 else (parent2.w_ih, parent1.w_ih)
child1.b_h, child2.b_h = (parent1.b_h, parent2.b_h) if random.random() < 0.5 else (parent2.b_h, parent1.b_h)
child1.w_ho, child2.w_ho = (parent1.w_ho, parent2.w_ho) if random.random() < 0.5 else (parent2.w_ho, parent1.w_ho)
child1.b_o, child2.b_o = (parent1.b_o, parent2.b_o) if random.random() < 0.5 else (parent2.b_o, parent1.b_o)
else:
child1, child2 = parent1, parent2 # 交叉しない
return child1, child2
def _mutate(self, individual):
# 各重み・バイアスを突然変異確率でランダムな値に置き換える
for w in [individual.w_ih, individual.b_h, individual.w_ho, individual.b_o]:
if random.random() < MUTATION_RATE:
w += np.random.uniform(-0.1, 0.1, w.shape)
main関数
def main():
# 教師データの生成
teacher_inputs = np.random.uniform(-5, 5, (NUM_TEACHER_DATA, NUM_INPUT))
teacher_outputs = np.array([target_function(x[0], x[1]) for x in teacher_inputs])
# テストデータの生成
test_inputs = np.random.uniform(-5, 5, (NUM_TEACHER_DATA, NUM_INPUT))
test_outputs = np.array([target_function(x[0], x[1]) for x in test_inputs])
ga = GeneticAlgorithm()
elite_errors = []
print("学習開始...")
for gen in range(GENERATIONS):
ga.run_generation(teacher_inputs, teacher_outputs)
# 最も優れた個体(エリート)を見つける
elite = max(ga.population, key=lambda ind: ind.fitness)
# テストデータでエリートの誤差を評価
test_error = 0.0
for i in range(len(test_inputs)):
prediction = elite.predict(test_inputs[i])
test_error += (prediction - test_outputs[i]) ** 2
mean_squared_error = test_error / len(test_inputs)
elite_errors.append(mean_squared_error)
if (gen + 1) % 10 == 0:
print(f"世代: {gen + 1}, テスト誤差 (MSE): {mean_squared_error:.6f}")
# 結果のプロット
plt.plot(elite_errors)
plt.title("Elite Individual's Error on Test Data")
plt.xlabel("Generation")
plt.ylabel("Mean Squared Error")
plt.grid(True)
plt.savefig("ga_nn_learning_curve.png")
plt.show()
if __name__ == '__main__':
main()
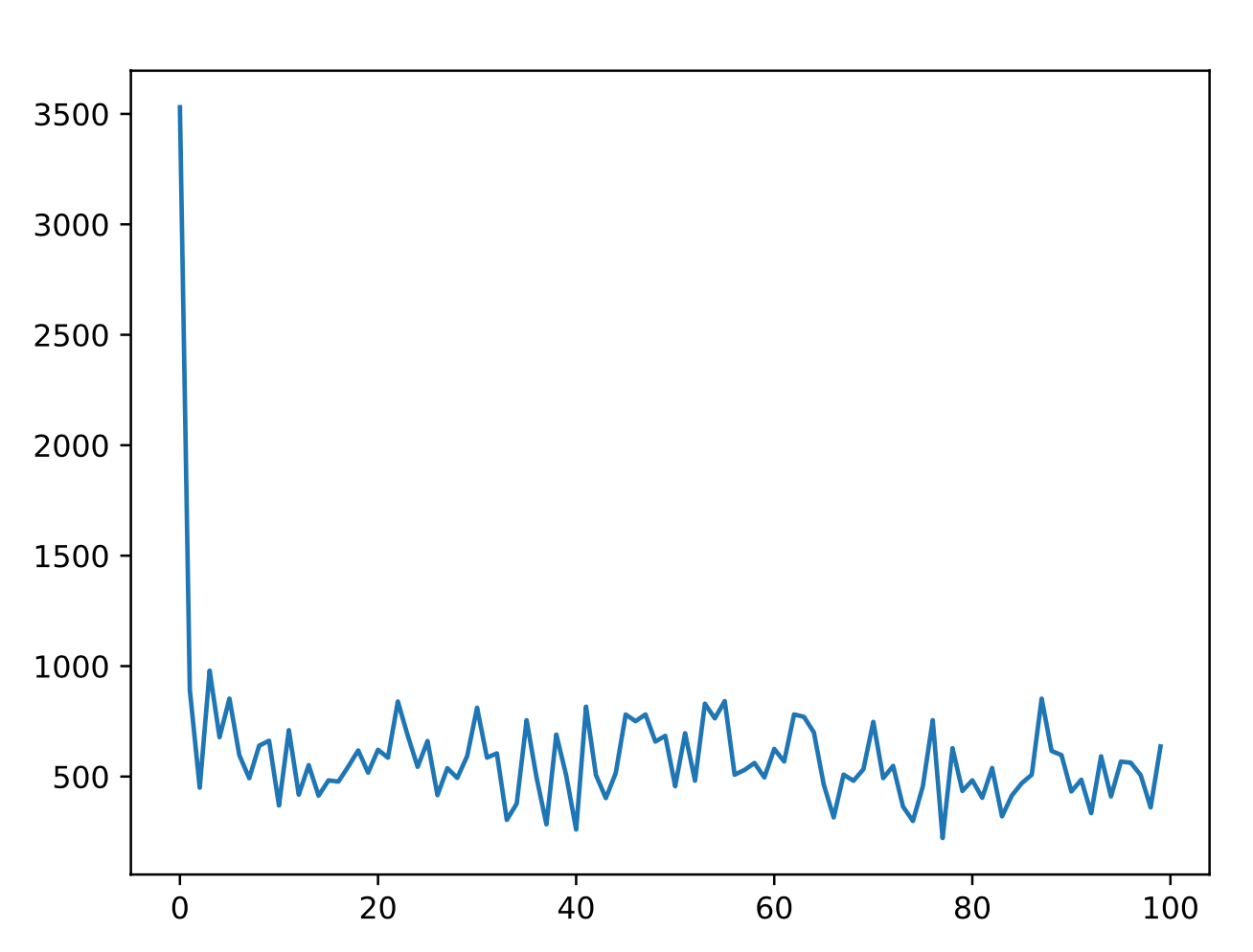
実験結果
各世代で最も適応度の高かった個体(エリート)をテストデータで評価し、その平均二乗誤差の推移をプロットしました。世代が進むにつれて誤差が減少し、NNが関数を学習している様子が確認できます。