EMアルゴリズム（2）：変分下界とKLダイバージェンス

EMアルゴリズムがなぜ対数尤度を増加させることができるのかを理解するために、「変分下界（Evidence Lower Bound, ELBO）」と「KLダイバージェンス（Kullback-Leibler Divergence）」という概念を導入します。

変分下界 (Evidence Lower Bound, ELBO)

EMアルゴリズムにおける変分下界 \(\mathcal{L}(\theta, \hat{\theta})\) は、以下のように定義されます。

\[ \mathcal{L}(\theta, \hat{\theta}) = \int p(z|x,\hat{\theta}) \log \frac{p(x,z|\theta)}{p(z|x,\hat{\theta})}dz \]

この式は、対数尤度 \(\log p(x|\theta)\) と、隠れ変数 \(z\) の事後分布 \(p(z|x,\hat{\theta})\) と \(p(z|x,\theta)\) の間のKLダイバージェンスの関係から導出されます。

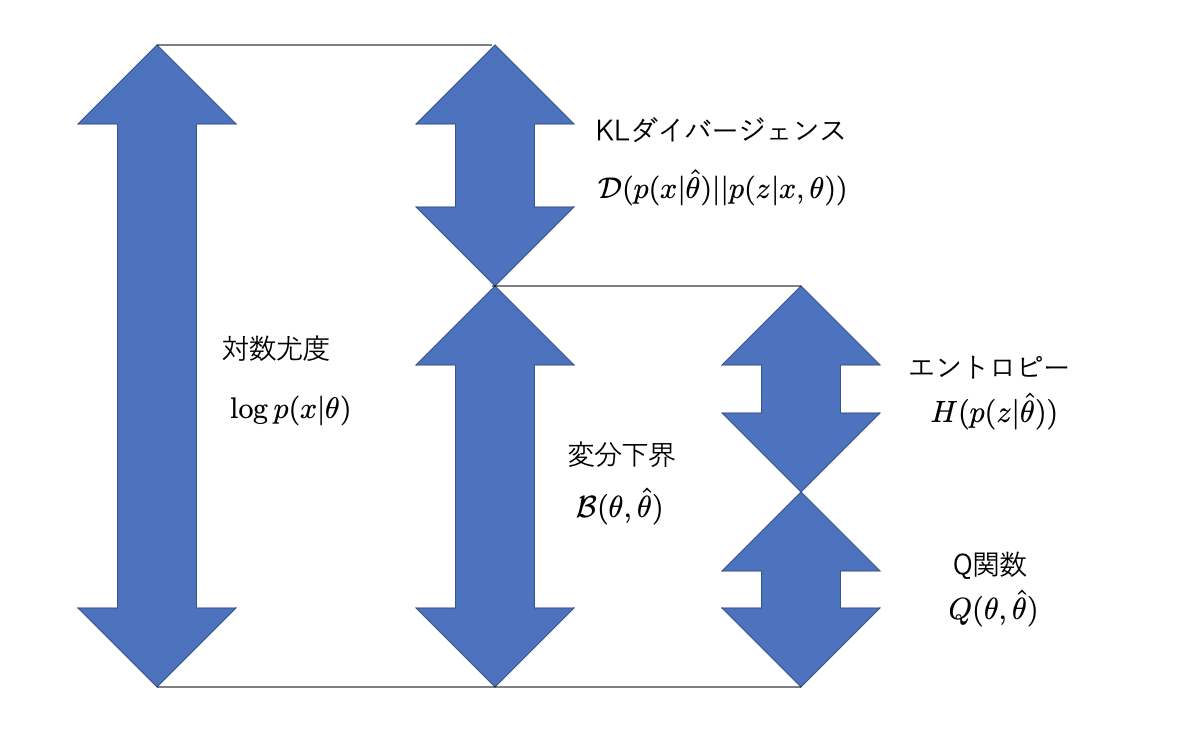
\[ \log p(x|\theta) = \mathcal{L}(\theta, \hat{\theta}) + KL(p(z|x,\hat{\theta}) || p(z|x,\theta)) \]

ここで、

変分下界 \(\mathcal{L}(\theta, \hat{\theta})\) は、Eステップで計算されるQ関数と、隠れ変数の事後分布のエントロピーの和として表現することもできます。

\[ \mathcal{L}(\theta, \hat{\theta}) = Q(\theta, \hat{\theta}) + H(p(z|x,\hat{\theta})) \]

KLダイバージェンス \(KL(q||p)\) は、2つの確率分布 \(q(x)\) と \(p(x)\) の間の「情報量的な距離」を測る尺度です。

\[ KL(q||p) = \mathbb{E}\_q[\log\frac{q(x)}{p(x)}] = \int q(x)\log \frac{q(x)}{p(x)}dx \]

KLダイバージェンスは以下の性質を持ちます。

EMアルゴリズムの各ステップは、対数尤度を単調に増加させます。これは、変分下界とKLダイバージェンスの関係から説明できます。

変分下界

Eステップ: 現在のパラメータ \(\hat{\theta}\) を固定し、隠れ変数 \(z\) の事後分布 \(p(z|x,\hat{\theta})\) を計算します。このステップでは、KLダイバージェンスが最小（0）になるように、つまり \(p(z|x,\hat{\theta})\) が \(p(z|x,\theta)\) に一致するように \(\theta\) を更新します。これにより、変分下界 \(\mathcal{L}(\theta, \hat{\theta})\) が対数尤度 \(\log p(x|\theta)\) に等しくなります。
Mステップ: Eステップで計算された \(p(z|x,\hat{\theta})\) を用いて、Q関数 \(Q(\theta, \hat{\theta})\) を最大化する新しいパラメータ \(\theta\) を見つけます。Q関数を最大化すると、変分下界 \(\mathcal{L}(\theta, \hat{\theta})\) も増加します。このとき、KLダイバージェンスは非負であるため、対数尤度 \(\log p(x|\theta)\) も増加します。

このように、EMアルゴリズムはEステップとMステップを繰り返すことで、対数尤度を単調に増加させていきます。