ベイズ推定において、事後分布を解析的に求めるためには、尤度関数と事前分布の組み合わせが重要になります。特定の尤度関数に対して、事後分布が事前分布と同じ関数形になるような事前分布を共役事前分布 (Conjugate Prior) と呼びます。共役事前分布を用いることで、事後分布の計算が非常にシンプルになります。
代表的な共役事前分布
ディリクレ分布 (Dirichlet Distribution)
多項分布のパラメータ(各カテゴリの確率)に対する共役事前分布は、ディリクレ分布 \(\mathcal{D}(\mu|\alpha)\) です。
\[ \mathcal{D}(\mu|\alpha) = \frac{\Gamma(\sum*{j=1}^{k}\alpha_j)}{\prod*{j=1}^k\Gamma(\alpha*j)}\prod*{j=1}^k\mu_j^{\alpha_j-1} \]ここで、\(\alpha = (\alpha_1, \dots, \alpha_k)\) はディリクレ分布のパラメータであり、\(\Gamma(\cdot)\) はガンマ関数です。ガンマ関数は階乗の概念を実数に拡張したもので、以下のように定義されます。
\[ \Gamma(x) = \int_0^\infty t^{x-1}e^{-t}dt \]ベータ分布 (Beta Distribution)
二項分布のパラメータ(成功確率)に対する共役事前分布は、ベータ分布 \(p(\mu|a,b)\) です。
\[ p(\mu|a,b) = \frac{1}{B(a,b)}\mu^{a-1}(1-\mu)^{b-1} \]ここで、\(a, b\) はベータ分布のパラメータであり、\(B(a,b)\) はベータ関数です。ベータ関数は以下のように定義されます。
\[ B(a,b) = \int_0^1\mu^{a-1}(1-\mu)^{b-1}d\mu \]ガンマ分布 (Gamma Distribution)
正規分布の**分散の逆数(精度パラメータ)**に対する共役事前分布は、ガンマ分布 \(\mathcal{G}(\lambda|\kappa,\xi)\) です。
\[ \mathcal{G}(\lambda|\kappa,\xi) = \frac{\xi^\kappa}{\Gamma(\kappa)}\lambda^{\kappa-1}\exp(-\xi\lambda) \]ここで、\(\lambda = 1/\sigma^2\) は精度パラメータ、\(\kappa\) は形状パラメータ、\(\xi\) は尺度パラメータ(またはレートパラメータの逆数)と呼ばれます。
補足: 正規分布の平均パラメータに対する共役事前分布は正規分布です。しかし、分散パラメータに対して正規分布を事前分布として用いると、事後分布が正規分布にならないため、共役ではありません。そこで、分散の逆数である精度パラメータを導入し、その共役事前分布としてガンマ分布を用いるのが一般的です。
ガンマ分布の余談
- \(\kappa=1\) のガンマ分布は指数分布と一致します。 \( \mathcal{G}(\lambda|1,\xi) = \frac{\xi^1}{\Gamma(1)}\lambda^{1-1}\exp(-\xi\lambda) = \xi\exp(-\xi\lambda) \) (\(\Gamma(1)=1\))
- \(\xi=\frac{1}{2}\) に設定し、\(\nu=2\kappa\) で定義されるパラメータで表したものはカイ二乗分布 \(\chi^2(\lambda|\nu)\) と呼ばれます。 \( \chi^2(\lambda|\nu) = \mathcal{G}(\lambda|\frac{\nu}{2},\frac{1}{2}) \)
正規-ガンマ分布 (Normal-Gamma Distribution)
正規分布の平均 \(\mu\) と精度 \(\lambda\) の両方を同時に推定する場合、その同時事前分布として正規-ガンマ分布 \(\mathcal{NG}(\mu,\lambda|\psi,\beta,\kappa,\xi)\) を用いることができます。これは、平均 \(\mu\) が正規分布に従い、精度 \(\lambda\) がガンマ分布に従うという構造を持ちます。
\[ \mathcal{NG}(\mu,\lambda|\psi,\beta,\kappa,\xi) = \mathcal{N}(\mu|\psi,(\beta \lambda)^{-1}) \mathcal{G}(\lambda|\kappa,\xi) \]一般的な確率分布と共役事前分布の対応
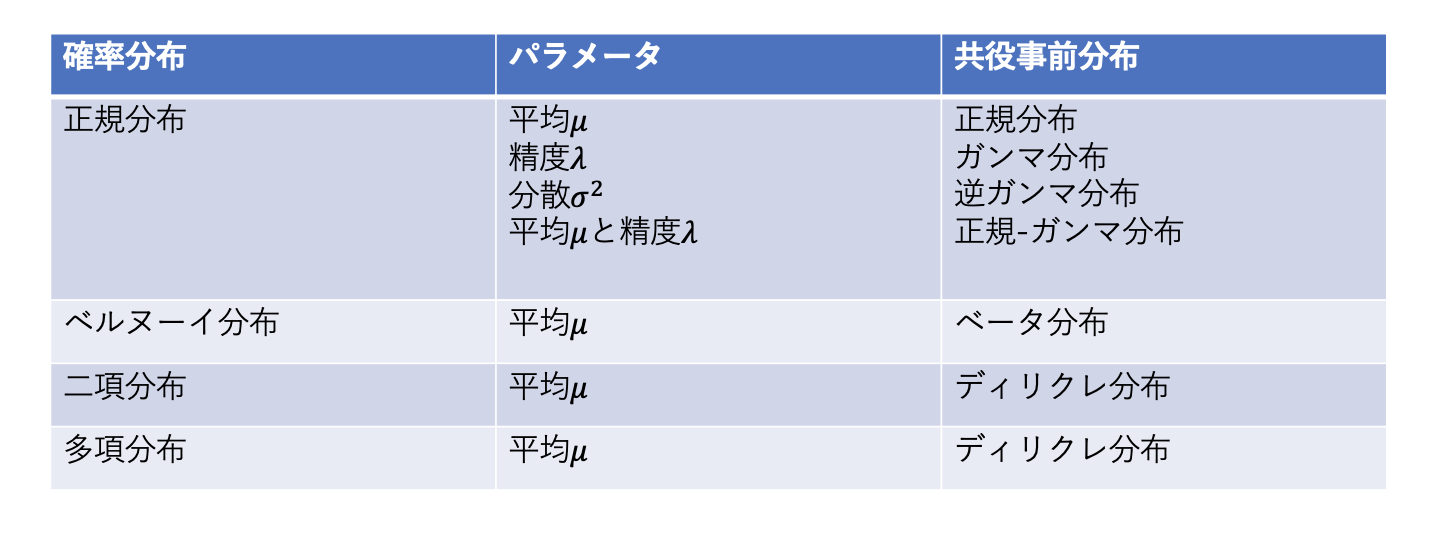
| 尤度関数(データ分布) | パラメータ | 共役事前分布 |
|---|---|---|
| ベルヌーイ分布 | 成功確率 \(\mu\) | ベータ分布 |
| 二項分布 | 成功確率 \(\mu\) | ベータ分布 |
| カテゴリカル分布 | 各カテゴリの確率 \(\mu\) | ディリクレ分布 |
| 多項分布 | 各カテゴリの確率 \(\mu\) | ディリクレ分布 |
| 正規分布 | 平均 \(\mu\) | 正規分布 |
| 正規分布 | 精度 \(\lambda\) | ガンマ分布 |
| 正規分布 | 平均 \(\mu\), 精度 \(\lambda\) | 正規-ガンマ分布 |
参考
- 手塚 太郎, 『しくみがわかるベイズ統計と機械学習』, 講談社 (2017)