深層学習モデルにおいて、確率分布からサンプリングされた変数を扱う場合、そのサンプリング操作は通常微分不可能です。そのため、誤差逆伝播法(バックプロパゲーション)を用いて勾配を計算し、モデルのパラメータを更新することができません。
この問題を解決するために、D. P. KingmaとM. Wellingが変分オートエンコーダ(VAE)の論文で導入した手法が、リパラメータ化トリック (Reparameterization Trick) です。
原理
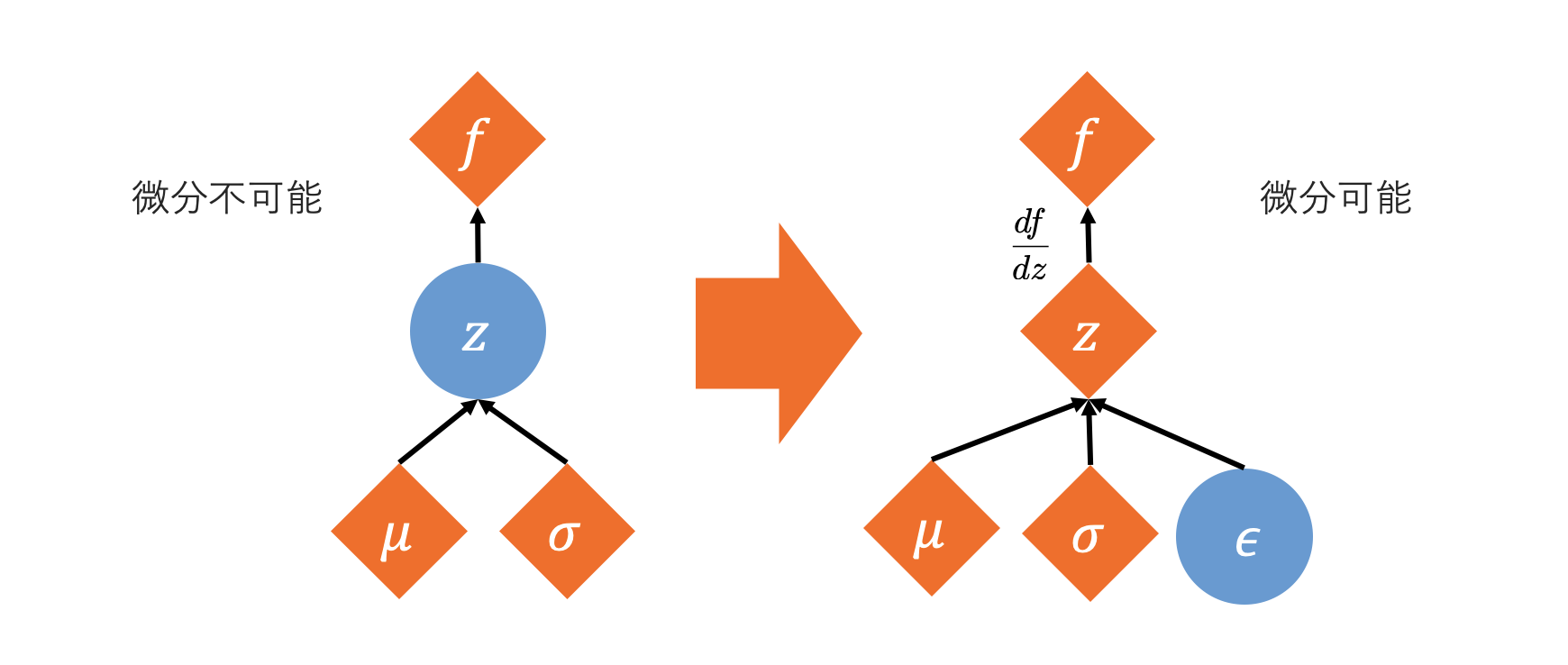
リパラメータ化トリックは、確率分布からのサンプリング操作を、パラメータに依存しないランダムノイズと、パラメータに依存する決定的な変換に分離することで、微分可能にする手法です。
例えば、平均 \(\mu\)、分散 \(\sigma^2\) の正規分布 \(\mathcal{N}(\mu, \sigma^2)\) から確率変数 \(z\) をサンプリングする場合を考えます。
\[ z \sim \mathcal{N}(\mu, \sigma^2) \]このサンプリング操作は微分不可能です。しかし、標準正規分布 \(\mathcal{N}(0, 1)\) からサンプリングされたランダムノイズ \(\epsilon\) を用いると、\(z\) は以下のように表現できます。
\[ z = \mu + \sigma \odot \epsilon \]\[ \text{ここで } \epsilon \sim \mathcal{N}(0, 1) \](\(\odot\) は要素ごとの積を表します。多次元の場合、\(\sigma\) は標準偏差のベクトルまたは共分散行列の平方根に対応します。)
この変換により、\(z\) は \(\mu\) と \(\sigma\) に対して決定的な関数となり、\(\mu\) と \(\sigma\) はニューラルネットワークの出力として微分可能になります。ランダム性は \(\epsilon\) にカプセル化され、勾配は \(\mu\) と \(\sigma\) を通じて逆伝播できるようになります。
PyTorchでのリパラメータ化トリックを用いたサンプリング
PyTorchの torch.distributions モジュールは、リパラメータ化トリックをサポートしている分布を提供しています。Normal クラスなどの分布オブジェクトは、rsample() メソッドを通じてリパラメータ化トリックを用いたサンプリングをサポートしています。
import torch
from torch.distributions import Normal
# ニューラルネットワークの出力として得られた平均と標準偏差
# 例として、mu=0, sigma=1 の正規分布を考える
mu = torch.tensor(0.0, requires_grad=True)
sigma = torch.tensor(1.0, requires_grad=True)
# 正規分布オブジェクトを作成
m = Normal(mu, sigma)
# rsample() メソッドを使ってサンプリング
# このサンプリングはリパラメータ化トリックが適用されるため、勾配が計算可能
z = m.rsample()
print(f"サンプリングされたz: {z}")
print(f"zの勾配計算可能フラグ: {z.requires_grad}") # Trueになる
m.has_rsample プロパティを確認することで、その分布がリパラメータ化トリックをサポートしているかどうかを判別できます。
print(f"Normal分布はrsampleをサポートしているか: {m.has_rsample}") # True
リパラメータ化トリックは、VAEだけでなく、強化学習の確率的方策勾配法など、確率的な要素を含む深層学習モデルの学習において非常に重要な技術です。
参考
- Kingma, D. P., & Welling, M. (2013). “Auto-Encoding Variational Bayes”. arXiv preprint arXiv:1312.6114.
- ReNom, 変分オートエンコーダ